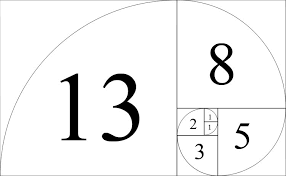
Even a casual observer will be impressed with the remarkable diversity, complexity and beauty of the natural world. A closer investigation will reveal a mathematical order and structure that at first may appear random. This mathematical order is related to the Fibonacci Sequence of numbers and the resulting Golden Spiral, Golden Ratio and Golden Angle. These topics are discussed in greater detail in the section titled “Spirals in Mathematics”. Simply to review, the next number in the Fibonacci Sequence, 0,1,1,2,3,5,8,13,21,34,55… is the sum of the preceding two numbers. The Golden Ratio is the proportional relationship between two successive Fibonacci numbers (e.g. 34 to 21 or as a ratio, 1: .618) and the Golden Spiral is a graphic display of the Fibonacci Sequence.

First, let’s look at the number of petals on a variety of flowers.

One-petalled white calla lily

Five-petalled columbine

Thirteen-petalled black eyed susan

34 petalled ordinary field daisies

You will notice that in each flower example, the number of petals corresponds to one of the Fibonacci Sequence numbers.

We can also see Fibonacci numbers associated with plant growth. New shoots of a plant commonly grow out at an axil, a point where a leaf has grown out of the main stem. A schematic diagram of a simple plant, the sneezewort, shows some interesting numbers. If we draw horizontal lines through each axil, you will notice that the number of leaves and the number of branches are Fibonacci Sequence numbers.

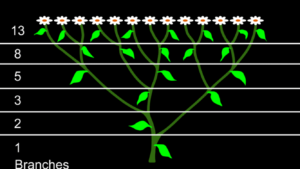
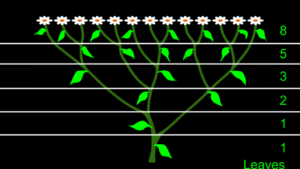
For illustration purposes, the schematic diagrams above are presented as if the plant was flat but actually, a majority of plant leaves and shoots spiral around the main stem. Phyllotaxis or phyllotaxy refers to the pattern or arrangement of leaves on the stem or branch of a plant. It is fairly common that the spiral arrangement of leaves on a plant is related to the Golden Ratio and the Golden Angle. You will recall that the Golden Ratio of two consecutive Fibonacci numbers is the ratio of 1: .618. If we apply the Golden Ratio to a circle, we see that the 360° circle is proportionally divided into two arcs, 360° X .618 equals 222.5° and the remaining arc is 137.5°.

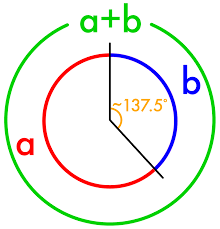
The Golden Angle is 137.5 degrees. It is fairly common, in many types of plants, that this is the angle at which adjacent leaves are positioned around the stem.

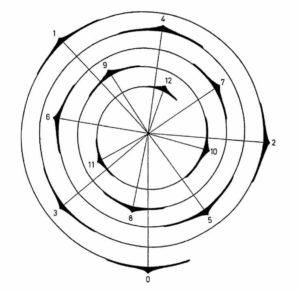
The positioning of leaves at this 137.5 degree angle around the stem minimizes the blockage of sunlight and rain falling down on the plant and therefore has a beneficial effect on the plant’s growth and survivability. It should be noted that the 137.5 degree positioning of leaves does not apply in all cases. These phyllotaxis observations are not considered “rules of nature” but rather as remarkable prevailing tendencies. The application of the Golden Angle observed here in botany will reappear in the section “Spirals in Architecture.”